Основания высот и медиан треугольника ABC лежат на окружности девяти точек ω₁ (см. задачу 152511). Прямая Эйлера MH является линией центров этой окружности и описанной окружности ω треугольника ABC (см. задачу 164414). Поэтому достаточно доказать, что точки A', B' и C' принадлежат радикальной оси ω и ω₁ (см. рис.).

  Докажем этот факт для точки C' (доказательство для остальных точек аналогично). Покажем, что CC' – касательная к окружности ω.   Первый способ. Поскольку прямые CC₁ и A₀B₀ перпендикулярны и отрезок CC₁ делится средней линией A₀B₀ пополам, то точки C и C₁ симметричны относительно прямой B₀C', следовательно,  ∠C'CA₀ = ∠C'C₁A₀  и  ∠CB₀A₀ = ∠C₁B₀A₀.

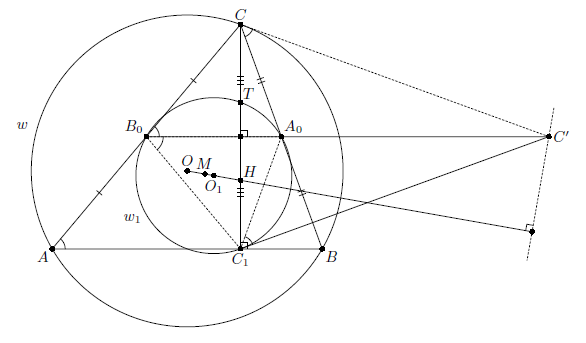
  Поскольку C₁C' – касательная к окружности ω₁, то  ∠A₀B₀C₁ = ∠A₀C₁C'. Из симметрию точек C и C₁ относительно B₀C' и параллельности прямых AB и A₀B₀ следует, что  ∠BAC = ∠A₀B₀C = ∠C'B₀C₁ = ∠A₀C₁C' = ∠C'CA₀,  то есть CC' – касательная к окружности ω.   Второй способ. Описанная окружность и окружность девяти точек гомотетичны с центром в точке H и коэффициентом ½. При этой гомотетии касательная к окружности ω в точке C перейдёт в касательную к ω₁ в точке T – середине отрезка CH. Эти касательные образуют с отрезком CC₁ равные углы. Касательные к ω₁ в точках T и C₁ также образуют с CC₁ равные углы. Следовательно, и касательные к окружностям ω и ω₁ в точках C и C₁ соответственно образуют с CC₁ равные углы. Значит, точка пересечения касательных лежит на серединном перпендикуляре к CC₁, то есть на A₀B₀.   В силу симметрии C'C = C'C₁,  то есть степени точки C' относительно окружностей ω и ω₁ равны. Следовательно, точка C' принадлежит радикальной оси этих окружностей, что и требовалось.

Ответ задачи отсутствует