Заметим, что  ∠CAB = ∠ACB = ∠APB = ∠BPC = ∠APC' = ∠CPA' = 60°,  ∠PBC = ∠PAC = ∠PC'A,  ∠PBA = ∠PCA = ∠PA'C  (см. рис.). Следовательно, следующие пары треугольников подобны:  BPC' и A'PB;  C'PA и APB';  A'PC и CPB'.

  Из первого подобия следует, что  BP² = C'P·A'P,  из второго:  AP² = C'P·B'P,  из третьего:  CP² = B'P·A'P.  Вычислим площадь треугольника A'B'C' как сумму площадей треугольников C'B'P, C'A'P и A'B'P (используя тот факт, что углы при вершине P этих треугольников равны 120°):

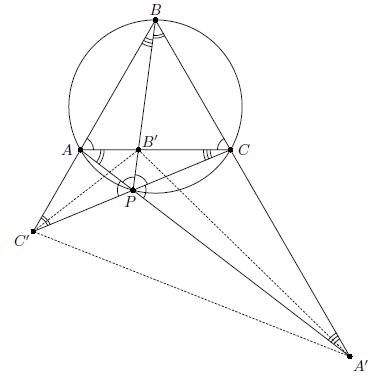
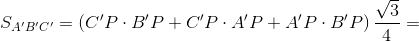
    где a – длина стороны треугольника ABC. Действительно,  AP² + BP² + CP² = 2a²  (см. задачу 153114 или задачу 157080). Поскольку 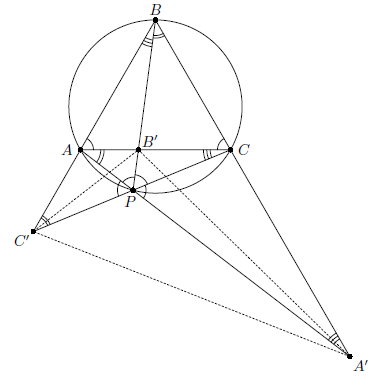    то S_A'B'C' = 2.