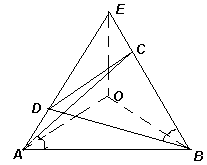
Продлим стороны AD и ВС до их пересечения в некоторой точке Е, тогда треугольник АВЕ – равносторонний (см. рис.). Докажем, что  ВС = ED.  Это можно сделать различными способами.

 Первый способ. В треугольниках АВС и ВЕD:  АВ = ВЕ;  ∠СAВ = ∠DВЕ,  ∠AВC = 60° = ∠ВЕD.  Таким образом, эти треугольники равны по второму признаку. Следовательно,  ВС = ED.  Второй способ. Пусть О – центр треугольника АВЕ. При повороте с центром О на угол 120° образами вершин А и В являются вершины В и Е соответственно, тогда образом луча АС – луч BD (из равенства  ∠СAВ = ∠CBD).  Так как образом стороны ВЕ при этом повороте является сторона ЕА, то образом точки С является точка D. Следовательно,  ВС = ED.   Таким образом,  AD + CB = AD + ED = АЕ = AB.

Ответ задачи отсутствует