Достаточно доказать, что середина K отрезка MN равноудалена от катетов AC и BC треугольника ABC.  Первый способ. Пусть общая касательная к двум окружностям, проведённая через точку K, пересекает прямые AC и BC, в точках P и Q соответственно (рис. слева). Прямоугольные треугольники AKP и QKB очевидно подобны, а так как их вписанные окружности равны, то и эти треугольники равны. Значит, равны и их высоты, опущенные из общей вершины K, то есть расстояния от K до прямых AC и BC.

  Второй способ. Проведём через центры O₁ и O₂ окружностей прямые, параллельные ближайшим катетам, до пересечения в точке L (рис. справа). Углы O₁LO₂ и O₁KO₂ прямые, значит, четырёхугольник O₁LO₂K вписанный. Поэтому углы O₁LK и O₂LK равны как опирающиеся на равные хорды. Следовательно, LK – биссектриса угла O₁LO₂, то есть точка K равноудалена от прямых O₁L и O₂L, а значит, и от прямых AC и BC (расстояние между прямыми O₁L и AC, как и расстояние между прямыми O₂L и BC, равно радиусу исходных окружностей).  Третий способ. Точка K равноудалена от окружностей, а значит, существует поворот с центром в точке K, переводящий первую окружность (касающуюся катета AC) во вторую (касающуюся катета BC). Очевидно, это поворот на 90°. При этом повороте прямая AC переходит в перпендикулярную ей прямую, касающуюся второй окружности, то есть в прямую BC. Значит, эти две прямые равноудалены от центра поворота K.

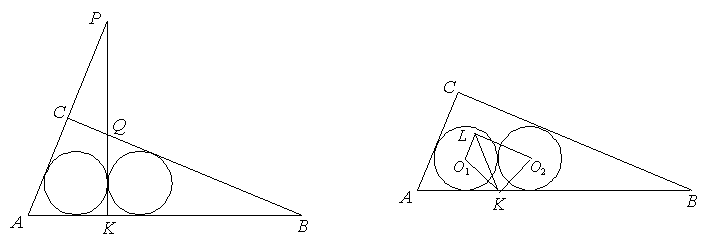
Ответ задачи отсутствует