Задача
Две окружности пересекаются в точках A и B. Их общая касательная (та, которая ближе к точке B) касается окружностей в точках E и F. Прямая AB пересекает прямую EF в точке M. На продолжении AM за точку M выбрана точка K так, что KM = MA. Прямая KE вторично пересекает окружность, содержащую точку E, в точке C. Прямая KF вторично пересекает окружность, содержащую точку F, в точке D. Докажите, что точки C, D и A лежат на одной прямой.
Решение
ME² = MB·MA = MF², то есть ME = MF. Далее можно рассуждать по-разному. Первый способ. Диагонали четырёхугольника AEKF делят друг друга пополам, то есть AEKF – параллелограмм.
∠CAE = ∠FEK (оба они равны углу между хордой CE и касательной FE). Аналогично ∠DAF = ∠EFK. Поэтому сумма трёх углов с вершиной A равна сумме углов треугольника EFK, то есть 180°. Значит, точки C, D и A лежат на одной прямой. Второй способ. ME·MF = MB·MA = MB·MK, следовательно, четырёхугольник BEKF – вписанный. Кроме того, KE·KC = KB·KA = KF·KD, поэтому точки E, B, F переходят в C, A, D при инверсии с центром K и радиусом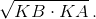 
А инверсия переводит окружность BEKF, проходящую через её центр, в прямую.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь