Для натуральных n и k введём обозначения  f(n) = n – S(n)  и  f ^k(n) = f(f(...(n)...))  (k раз). При увеличении числа n на 1, число S(n) либо увеличивается на 1 (если n не заканчивается на 9), либо уменьшается. Это значит, что функция f не убывает, причём  f(n + 10) > f(n)  при всех n.   Первый способ. Выберем такое натуральное d, что  10^d > 20d(n + 1),  и положим   k = 10^d.  Пусть  b₀ = 10^k – 1,  c₀ = 10^k – k,  b_i = f ⁱ(b₀),  c_i = f ⁱ(c₀).  Докажем, что  b_n > c_n > b_n+1.     (*)

  Так как  S(c₀) ≤ 9k,  по индукции получаем  c_i ≥ 10^k – k – 9ki.  При  i ≤ n + 1  имеем  (9i + 1)k ≤ 10ki ≤ 10^d+1(n+1) < 10^2d,  а значит, в числе c_i хотя бы

k – 2d  первых цифр – девятки. Поэтому  S(c_i) ≥ 9(k – 2d),  откуда (опять по индукции)  c_i ≤ 10^k – k – 9(k – 2d)i.  Итак,

10^k – (9i + 1)k ≤ c_i ≤ 10^k – k – 9(k – 2d)i.

  Аналогично получаются оценки  10^k – 9ki – 1 ≤ b_i ≤ 10^k – 1 – 9(k – 2d)i.

  Таким образом, для доказательства неравенства  c_n < b_n  достаточно проверить, что  10^k – k – 9(k – 2d)n < 10^k – 9kn – 1,  то есть  k > 18dn + 1.  Это верно в силу выбора d. Чтобы доказать неравенство  b_n+1 < c_n,  достаточно проверить, что

10^k – 1 – 9(k – 2d)(n + 1) < 10^k – (9n + 1)k,  то есть  8k + 1 > 18d(n + 1),  что тоже верно.

  Поскольку  c_n = f ⁿ(c₀),  то число c_n является n-хорошим. В то же время, если  x ≤ b₀,  то  f ⁿ⁺¹(x) ≤ f ⁿ⁺¹(b₀) = b_n+1 < c_n.  Если же  x > b₀,  то

f (x) ≥ f(10^k) = b₀,  и поэтому  f ⁿ⁺¹(x) ≥ f ⁿ(b₀) = b_n > c_n.  Следовательно, c_n не является (n+1)-хорошим.   Второй способ. Предположим противное: любое n-хорошее число x является (n+1)-хорошим. Это значит, что  x = f ⁿ⁺¹(y)  при некотором y. Тогда число  f(y) является n-хорошим – а значит, и (n+1)-хорошим; из этого, в свою очередь следует, что x является (n+2)-хорошим. Аналогично показывается, что любое n-хорошее число является (n+k)-хорошим при всех натуральных k; назовём такое число просто хорошим.

  Выберем натуральное k > 3·10ⁿ и оценим количество D_k хороших k-значных чисел двумя способами.

  1. Для каждого числа  y ∈ [2·10^k–1, 10^k)  число  g(y) = f ⁿ(y)  является хорошим. Кроме того,  g(y) ≥ y – 9kn ≥ y – 10^k–1 ≥ 10^k–1,  то есть g(y) – хорошее k-значное число. С другой стороны, уравнение  f(x) = a  имеет не более 10 решений при любом a, поэтому уравнение  g(y) = a  имеет не более 10ⁿ решений. Значит,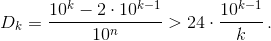  

  2. Пусть x – хорошее k-значное число. Тогда  x = f ^10k(y)  при некотором y. Так как  f ^10k(y) ≤ y – 10^k,  число y хотя бы (k+1)-значно. Пусть s – наименьшее число, для которого  f ^s(y)  является k-значным числом. Тогда  f ^s–1(y) ≥ 10^k,  откуда  f ^s(y) = f(f ^s–1(y)) ≥ f(10^k) = 10^k – 1.  Таким образом,

f ^s(y) = 10^k – 1,  то есть любое k-значное хорошее число есть  f ^t(10^k – 1)  при некотором t.

  Покажем, что число  f ^t(10^k – 1)  может являться k-значным лишь при 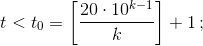    отсюда будет следовать, что  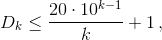   что противоречит оценке из предыдущего пункта. Положим  b₀ = 10^k – 1,  b_i = f ⁱ(b₀).  Достаточно доказать, что  b_t0 < 10^k–1.

  Предположим противное; тогда все числа b_i при  i ≤ t₀  являются k-значными. Оценим количество таких индексов  i < t ₀,  что  b_i – b_i+1 < k  (то есть  S(b_i) < k).  Цифры любого такого числа b_i образуют последовательность из k неотрицательных целых чисел с суммой, не большей  k – 1.  Но существует ровно 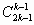   таких последовательностей (это легко выводится из задачи 130719 б). Значит, и требуемых индексов не больше чем  .

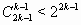  Итак, в последовательности b₀, b₁, ..., b_t0  следующее число меньше предыдущего хотя бы на k как минимум в  t₀ – 2^2k–1  случаях. Заметим, что     поскольку  k·2^2k–1 ≤ 10^k.  Поэтому  b_t0 ≤ b₀ – (t₀ – 2^2k–1)k ≤ 10^k – 10^k = 0.  Противоречие.

Верно.