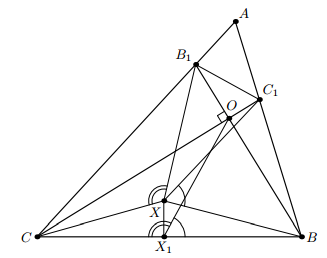
Решение 1:   Пусть X₁ – проекция точки X на прямую BC, а O – точка пересечения прямых BB₁ и CC₁. Тогда треугольник C₁BO подобен треугольнику XBX₁ по двум углам, значит,  BC₁ : BX = BO : BX₁.  Следовательно, подобны и треугольники BC₁X и BOX₁ – по углу и отношению прилежащих к нему сторон. Значит,

∠BXC₁ = ∠BX₁O.

  Аналогично  ∠B₁XC = ∠OX₁C  (см. рис.). Поэтому   ∠BXC₁ + ∠CXB₁ = ∠BX₁O + ∠OX₁C = 180°.  Отсюда

∠C₁XB₁ = 180° – ∠BXC = ∠XBC + ∠XCB = ∠ABB₁ + ∠ACC₁ = ∠BOC – ∠BAC = 90° – ∠A.

Решение 2:   Лемма. Если проекции точки P на стороны четырёхугольника ABCD лежат на одной окружности, то прямые, симметричные прямым AP, BP, CP и DP относительно биссектрис соответствующих углов, пересекаются в одной точке.

  Доказательство. Так как проекции P на стороны лежат на одной окружности, точки K, L, M и N, симметричные P относительно AB, BC, CD и DA соответственно, также лежат на одной окружности Ω. Поскольку  AK = AP = AN,  серединный перпендикуляр к отрезку KN совпадает с биссектрисой угла KAN, которая симметрична AP относительно биссектрисы угла BAD. Следовательно, все четыре указанные в условии леммы прямые проходят через центр окружности Ω.   Рассмотрим четырёхугольник BCB₁C₁. Его диагонали по условию перпендикулярны. Согласно задаче 157028 проекции точки O их пересечения на стороны четырёхугольника лежат на одной окружности.

  Прямые BX и CX симметричны прямым BB₁ и CC₁ относительно биссектрис углов B и C соответственно. Поэтому из леммы следует, что прямые B₁X и C₁X симметричны B₁B и C₁C относительно биссектрис углов CB₁C₁ и BC₁B₁ соответственно. Отсюда

∠B₁XC₁ = 180° – ∠XB₁C₁ – ∠XC₁B₁ = 180° – ∠CB₁O – ∠BC₁O = 180° – (90° + ∠A) = 90° – ∠A.

Ответ задачи отсутствует