Задача
В остроугольном неравнобедренном треугольнике ABC проведены высоты AA1, BB1, CC1 и отмечены точки A2, B2, C2, в которых вневписанные окружности касаются сторон BC, CA, AB соответственно. Прямая B1C1 касается вписанной окружности треугольника. Докажите, что точка A1 лежит на описанной окружности треугольника A2B2C2.
Решение
Пусть H, I и O – соответственно ортоцентр, центр вписанной окружности ω и центр описанной окружности Ω треугольника ABC, r – радиус ω, A', B' и C' – точки касания сторон BC, AC и AB с вписанной окружностью, IA, IB и IC – центры вневписанных окружностей, касающихся тех же сторон соответственно, а MA – середина BC.
Из условия следует, что четырёхугольник BC1B1C описан около ω и вписан в окружность с диаметром BC. Как известно, во вписанно-описанном четырёхугольнике точка пересечения диагоналей лежит на прямой, соединяющей центры вписанной и описанной окружностей (это следует, например, из того факта, что точка пересечения диагоналей является полюсом прямой, соединяющей точки пересечения продолжений противоположных сторон, относительно обеих окружностей). Таким образом, точки H, I и MA лежат на одной прямой (рис. слева). Докажем, что
r = 2OMA. Первый способ. Пусть A3 – точка окружности ω, диаметрально противоположная точке A'. Как известно, точки A, A3 и A2 лежат на одной прямой. Кроме этого, MA – середина A2A'. Значит, IMA – средняя линия треугольника A2A'A3. Из этого следует, что HI || AA3, то есть AA3IH – параллелограмм, и r = A3I = AH = 2OMA (невырожденность параллелограмма следует из неравнобедренности треугольника ABC).
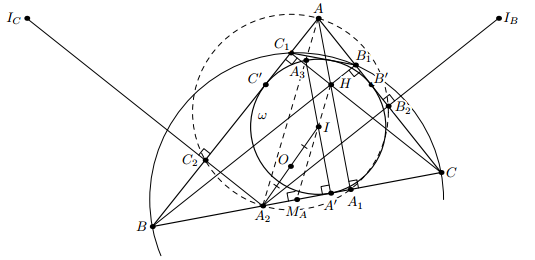
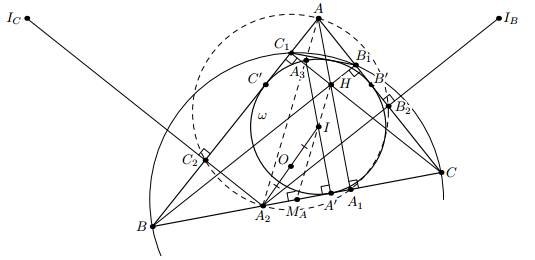
По условию окружность ω является вневписанной для треугольника AB1C1. Значит, при преобразовании подобия, переводящем треугольник AB1C1 в треугольник ABC, окружность ω переходит в ωA. Отсюда AB'/AT = cos∠A, то есть TB' ⊥ AC, и TB' проходит через I. Поскольку ∠TIC' = ∠A = ∠COMA, прямоугольные треугольники TIC' и COMA подобны (рис. справа). Более того, TC' = TB + BC' = BA2 + CA2 = BC = 2CMA, так что коэффициент подобия равен 2. Поэтому OMA = ½ IC' = r/2. Следовательно, отрезок MAO является средней линией треугольника IA'A2 (он проходит через середину A'A2, параллелен IA' и равен ½ IA').
Итак, точка A2 симметрична точке I относительно точки O. Прямая ICC2 симметрична IC' относительно O; значит, она проходит через A2. Поэтому ∠A2C2C = 90°. Аналогично, ∠A2B2B = 90° = ∠AA1B. Это значит, что точки B2, C2 и A1 лежат на окружности с диаметром AA2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь