Задача
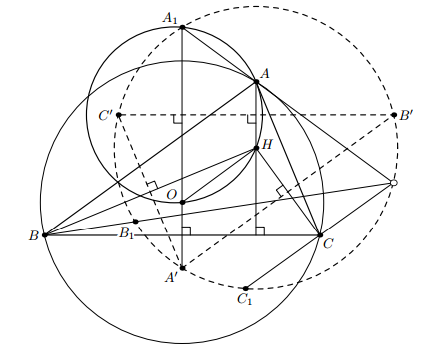
Пусть H и O – ортоцентр и центр описанной окружности треугольника ABC. Описанная окружность треугольника AOH, пересекает серединный перпендикуляр к BC в точке A1. Аналогично определяются точки B1 и C1. Докажите, что прямые AA1, BB1 и CC1 пересекаются в одной точке.
Решение
Рассмотрим треугольник A'B'C', образованный отражениями точки O относительно сторон треугольника ABC. Его вершины – центры описанных окружностей треугольников HBC, HCA и HAB; значит, его стороны – серединные перпендикуляры к AH, BH и CH, и они параллельны сторонам треугольника ABC. Значит, O – ортоцентр треугольника A'B'C' (см. рис.).
С другой стороны, поскольку стороны AH и A1O вписанного четырёхугольника AHOA1 параллельны, прямые AA1 и OH симметричны относительно серединного перпендикуляра к AH, то есть относительно B'C'; аналогичное утверждение выполняется для BB1 и CC1. Согласно задаче 155657 эти три прямые пересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь