Отметим на плоскости точки  A(0, 0),  A₁(0, 10),  B(9, 6),  B₁(4, 9),  C(5, 5),  D(15, 5)  и  B₂(9, 4)  (рис. слева). Нетрудно убедиться, что точки B₁ и B₂ симметричны относительно AC, а точки B₂ и B, а также A и A₁ – относительно CD. Поэтому фигура, составленная из треугольников AB₁C, ACD, CBD и BA₁D, представляет собой развёртку вырожденного тетраэдра ACDB₂ (он вырожден потому, что  ∠A₁DB + ∠BDC = ∠CDA).

  Чтобы устранить эту “неприятность”, чуть сдвинем точкуC"влево-вниз" вдоль серединного перпендикуляра к отрезкуBB₁(рис. справа). Для полученной точкиC₁сохраняется равенство  B₁C₁=BC₁,  но теперь для углов  α = ∠A₁DB,  β = ∠BDC₁  и  γ = ∠C₁DA  выполнены неравенства треугольника:  α + β > γ  по построению, а неравенства  α + γ > β  и  γ + β > α  сохраняются ввиду малости сдвига. Поэтому фигура, составленная из треугольниковA₁DB, BDC₁иC₁DA, представляет собой развёртку трёхгранного угла с вершинойD, то есть тетраэдра без одной грани. Недостающая грань равна треугольникуAB₁C₁, поэтому фигураAB₁C₁BA₁DBна рис. справа – развёртка тетраэдра. Как видим, она самопересекается.

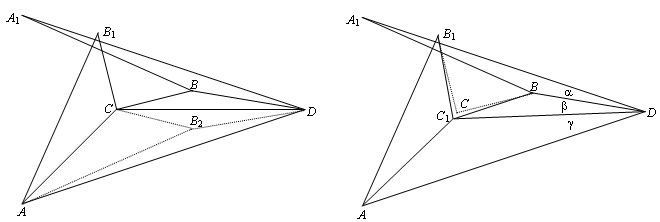
Ответ задачи отсутствует