Задача
Внутри параллелограмма ABCD выбрана точка Р так, что ∠АРВ + ∠СРD = 180°. Докажите, что ∠РВC = ∠РDC.
Решение
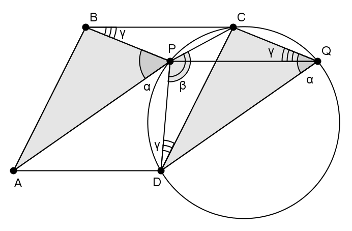
Построим параллелограмм BCQP (см. рис.). ∠DCQ = ∠АВP (углы с сонаправленными сторонами). Значит, равны треугольники CDQ и BAP. Следовательно, ∠CPD + ∠DQC = ∠CPD + ∠АРВ = 180°, то есть четырёхугольник CPDQ – вписанный.
Вписанные углы РDC и РQС равны. Значит, ∠РBC = ∠РQC = ∠РDC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет