Задача
На катетах AC и BC прямоугольного треугольника ABC отметили точки K и L соответственно, а на гипотенузе AB – точку M так, что AK = BL = a,
KM = LM = b и угол KML прямой. Докажите, что a = b.
Решение
Решение 1: Предположим, что a > b. Тогда из треугольника AKM получаем, что ∠AMK > ∠A. Следовательно, ∠B = 90° – ∠A > 90° – ∠AMK = ∠BML, и из треугольника BML получаем, что b > a. Противоречие.
Аналогично к противоречию приводит предположение a < b.
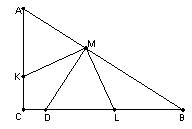
Решение 2: При повороте вокруг M на 90° точка K перейдёт в L, точка A – в некоторую точку D. При этом AM ⊥ DM, AK ⊥ DL. Отсюда следует, что D лежит на прямой BC, а ML – медиана, проведённая к гипотенузе прямоугольного треугольника DMB. Значит, она равна половине гипотенузы DB, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь