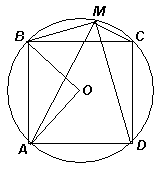
Пусть М не совпадает ни с одной из вершин квадрата (иначе, значение произведения равно нулю и не может быть наибольшим) и лежит на дуге ВС, O – центр описанной окружности (см. рис.). Заметим, что  ∠АМВ = ½ ∠АОВ = 45°.  Так как  S_AMB = ½ MA·MB sin∠AMB,  то  MA·MB = ^2S_AMB/_{sin 45°}.  Аналогично  MC·MD = ^2S_CMD/_{sin 45°},  значит,  MA·MB·MC·MD = 8S_AMB· S_CMD.

  Обозначим черезxрасстояние от точкиМдо прямойАВ, тогда расстояние отМдо прямойCDравно  1 –x.  Значит,  S_AMB= ½АВ·x=^x/₂,  а S_CMD= ½CD· (1 –x) = ½ (1 –x).  Таким образом,  MA·MB·MC·MD= 2x(1 –x).  Так как  0 <x< 1,  то полученное выражение принимает наибольшее значение при  x= ½.  Это значение равно ½.

0,5.