Задача
Решите систему уравнений: 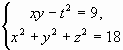 .
.
Решение
Первый способ. xy = 9 + t² ≥ 9 и x² + y² = 18 – z² ≤ 18. Следовательно, 18 ≥ x² + y² ≥ 2xy ≥ 18. Значит, все знаки неравенства должны обратиться в знаки равенства, то есть x² + y² = 2xy = 18, поэтому x = y = ±3.
Из первого уравнения системы и условия xy = 9 следует, что t = 0, а из второго уравнения и условия x² + y² = 18 следует, что z = 0. Второй способ. (x – y)² = x² + y² – 2xy = (18 – z²) – (9 + t²) = – z² – 2t².
Так как левая часть принимает только неотрицательные значения, а правая – только неположительные, то равенство возможно тогда и только тогда, когда х = y и t = z = 0. Подставив этот результат в любое из уравнений системы, получим, что x = y = ±3. Затем подстановкой полученных значений в другое уравнение убеждаемся, что они являются и его решением.
Ответ
(3, 3, 0, 0), (–3, –3, 0, 0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь