Пусть плоскость пересекла N рёбер призмы, тогда в её сечении получился N-угольник. Значит, эта плоскость пересекла и ровно N граней призмы. Сечение выпуклого многогранника не может иметь больше сторон, чем количество граней этого многогранника. Значит,  N ≤ 2017.

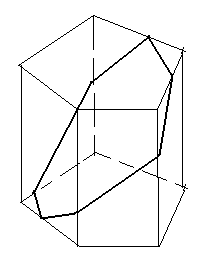
  Существование сечения, пересекающего все грани призмы, проще показать на примере прямой призмы с меньшим количеством граней, например, для пятиугольной призмы (см. рис.). Таким образом, наибольшее значение N равно 2017.