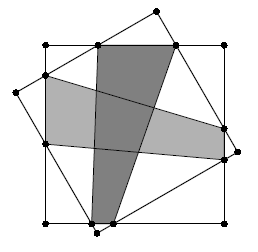
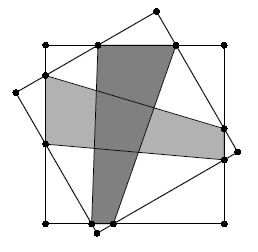
Обозначим точки пересечения сторон квадратов и продлим их стороны (см. рис.).

  Рассмотрим параллелограммыABCDиA₁B₁C₁D₁. Соответствующие стороны этих параллелограммов перпендикулярны, значит, углы параллелограммов равны. Кроме того, соответствующие высоты параллелограммов равны сторонам данных квадратов, то есть также соответственно равны.   Следовательно, параллелограммы равны и совмещаются композицией поворота на 90° и параллельного переноса, а соответствующие диагоналиBDиB₁D₁параллелограммов равны и перпендикулярны.   Аналогично доказывается равенство и перпендикулярность отрезковMPиLK.   Значит, диагонали четырёхугольниковKDLBиB₁MD₁Pсоответственно равны и пересекаются под одним и тем же углом, откуда (посколькуплощадь четырёхугольника равна половине произведения диагоналей на синус угла между ними) и следует утверждение задачи.

Ответ задачи отсутствует