Задача
В четырёхугольнике ABCD ∠B = ∠D = 90° и AC = BC + DC. Точка P на луче BD такова, что BP = AD.
Докажите, что прямая CP параллельна биссектрисе угла ABD.
Решение
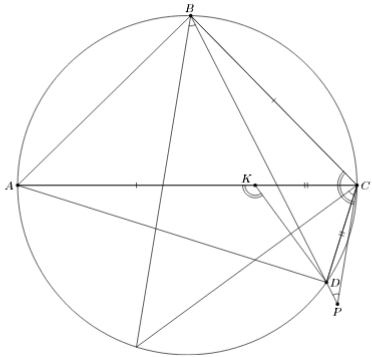
Из условия следует, что точки B и D лежат на окружности с диаметром AC. Пусть K – такая точка отрезка AC, что AK = BC (см. рис.). Тогда CK = CD, то есть ∠CKD = ∠CDK. Кроме того, треугольники BCP и AKD равны, поскольку AK = BC, AC = BP и ∠KAD = ∠CAD = ∠CBD = ∠CBP. Следовательно, ∠BCP = ∠AKP = 180° – ∠CKD = 90° + ½ ∠ACD = 90° + ½ ∠ABD, откуда ∠BCP + ½ ∠ABD + ∠CBP = 90° + ∠ABD + ∠CBP = 180°, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет