Задачи и олимпиады по математике

Задача

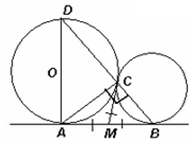
Две окружности касаются друг друга в точке C и прямой l в точках A и B. Прямая ВC пересекает вторую окружность в точке D.

Докажите, что угол BАD – прямой.

Решение

Пусть общая внутренняя касательная к данным окружностям пересекает прямую АВ в точке M (см. рис.).

Так как касательные, проведённые к окружности из одной точки, равны, то МА = МС = МВ. Значит, треугольникАВС– прямоугольный, ∠АСВ= 90°. Поэтому смежный с ним уголACD– также прямой, то естьAD– диаметр окружности. Следовательно, DA⊥AB.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления