Решение 1:Предположим, что  (cos x, cos y, cos z)  – арифметическая прогрессия. Тогда  2cos y = cos x + cos z.  Из условия следует, что  2sin y = sin x + sin z.  Возведём в квадрат каждое из этих равенств и почленно сложим. Получим:

4cos²y + 4sin²y = cos²x + 2cos x cos z + cos²z + sin²x + 2sin x sin z + sin²z  ⇔  cos(x – z) = 1  ⇔  x – z = 2πn,  n ∈ Z.  Следовательно,  sin x = sin(z + 2πn) = sin z,  что противоречит условию.

Решение 2:   На координатной плоскости рассмотрим точки  А(cos x, sin x),  В(cos y, sin y)  и  С(cos z, sin z).

  Если каждая из последовательностей  (cos x, cos y, cos z)  и  (sin x, sin y, sin z)  является арифметической прогрессией, то 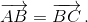    Из условия следует, что эти векторы не нулевые, следовательно, точки А, В и С лежат на одной прямой. С другой стороны, эти три точки лежат на единичной окружности. Одновременно это невозможно.

Не может.