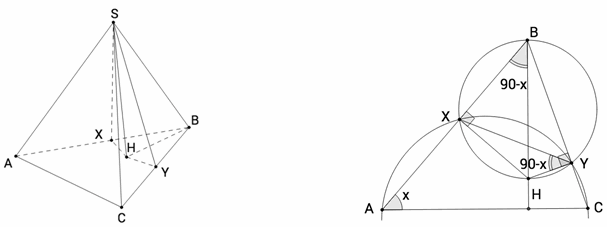
Решение 1:   Пусть H – проекция точки S на плоскость ABC, тогда по теореме о трёх перпендикулярах  HX ⊥ AB  и  HY ⊥ BC  (рис. слева).

  Рассмотрим треугольникABC(рис. справа). Пусть  ∠BАH = x.  ЧетырёхугольникAXYC– вписанный, следовательно, и  ∠BАH = x.  Кроме того, точкиXиYлежат на окружности с диаметромBH. Значит,  ∠АВH= ∠XYH= 90° –x.  Таким образом,  ∠АВH+ ∠BАH= 90°,  то есть  BH⊥АС.  Следовательно, и  BS⊥АС.

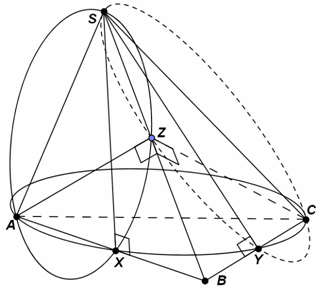
Решение 2:   Проведём высоту AZ в грани SAB (см. рис.). Точки X и Z лежат на окружности с диаметром AS. Значит,  BX·BA = BZ·BS.  Четырёхугольник AXYC – вписанный, поэтому  BY·BC = BX·BA = BZ·BS.

  Следовательно, точкиС, Y, ZиSтакже лежат на одной окружности. Значит,  ∠CZS= ∠CYS= 90°.   Таким образом,  BS⊥ZA  и  BS⊥ZС,  значит, прямаяBSперпендикулярна плоскостиAZC, поэтому  BS⊥AC.

Ответ задачи отсутствует