Задача
Дан многочлен f(x) = x4 + ax³ + bx² + cx. Известно, что каждое из уравнений f(x) = 1 и f(x) = 2 имеет четыре корня. Докажите, что если для корней первого уравнения выполняется равенство x1 + x2 = x3 + x4, то и для корней второго уравнения выполняется аналогичное равенство.
Решение
Первый способ. Пусть x1 + x2 = x3 + x4 = m. Тогда f(x) – 1 = (x – x1)(x – x2)(x – x3)(x – x4) = (x² – mx + x1x2)(x² – mx + x3x4).
Уравнение f(x) = 2 можно записать в виде (x² – mx + x1x2)(x² – mx + x3x4) = 1. Сделав замену y = x² – mx, получим уравнение
(y + x1x2)(y + x3x4) = 1. Так как уравнение f(x) = 2 имеет четыре корня, то это уравнение должно иметь два корня y1 и y2. При этом, два корня уравнения f(x) = 2 будут являться решениями уравнения x² – mx = y1, а еще два – решениями уравнения x² – mx = y2. Но в каждом из этих уравнений сумма корней равна m, поэтому для четырёх корней уравнения f(x) = 2 выполняется требуемое равенство. Второй способ. Пусть ½ (x1 + x2) = ½ (x3 + x4) = n. Рассмотрим многочлен g(x) = f(x + n), тогда корнями уравнения g(x) = 1 будут являться числа
αi = xi – n, i = 1, 2, 3, 4. При этом, α1 + α2 = α3 + α4 = 0, то есть эти числа попарно противоположны. Значит, функция
g(x) = (x – α1)(x – α2)(x – α3)(x – α4) = (x – α1)(x + α1)(x – α3)(x + α3) =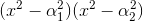 
является чётной. Следовательно, корни уравнения g(x) = 2 также попарно противоположны.
Корни уравнения f(x) = 2 получатся из соответствующих корней уравнения g(x) = 2 прибавлением числа n, поэтому они будут обладать требуемым свойством.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь