Задача
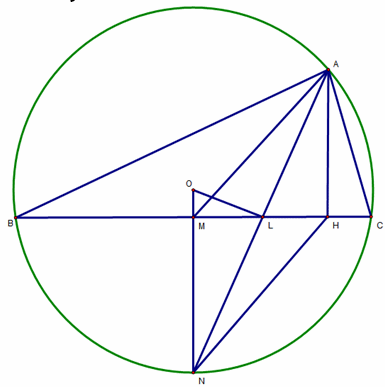
В треугольнике АВС проведены медиана АМ, биссектриса AL и высота AH.
Найдите радиус описанной окружности Ω треугольника АВС, если AL = t, AH = h и L – середина отрезка MH.
Решение
Продолжим биссектрису AL до её пересечения в точке N с окружностью Ω (см. рис.). Пусть O – центр Ω. Из равенства дуг BN и CN следует, что серединный перпендикуляр OM к стороне ВС проходит через точку N.
Ответ
t2/h.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет