Минимизация положительных чисел: олимпиадная задача
Задача
По кругу написано 100 ненулевых чисел. Между каждыми двумя соседними числами написали их произведение, а прежние числа стерли. Количество положительных чисел не изменилось. Какое минимальное количество положительных чисел могло быть написано изначально?
Решение
Оценка. Предположим, что положительных чисел было не более 33. Отрицательные числа в произведении могут образовываться, только если один из сомножителей положительный, причём каждое положительное число может участвовать не более чем в двух таких произведениях. Следовательно, отрицательных чисел не более 66. Но тогда всего чисел не более 99. Противоречие.
Пример для 34 положительных чисел. Расставим знаки следующим образом:
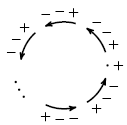
Ответ
34 числа.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет