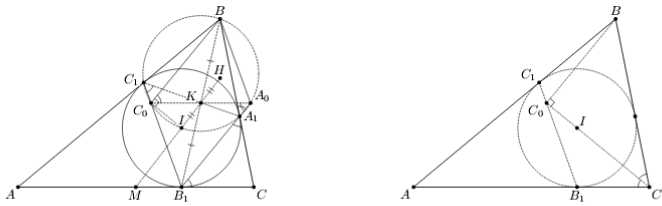
Рассмотрим описанную окружность треугольника A₀BC₀. Заметим, что точка I диаметрально противоположна точке B (поскольку  ∠BC₁I = 90°). Согласно решению задачи 208600 точки H и I симметричны относительно середины K отрезка A₀C₀, то есть достаточно доказать, что точки M, I и K лежат на одной прямой (рис. слева). Далее можно рассуждать по-разному.   Первый способ. Пусть T – точка касания вневписанной окружности треугольника ABC со стороной AC. Как известно, точка M – середина отрезка TB₁, а прямая BT проходит через точку вписанной окружности, диаметрально противоположную точке B₁. Следовательно, прямая MI содержит среднюю линию треугольника BB₁T, а значит, делит BB₁ пополам.

  Из равенства вписанных углов и теоремы об угле между касательной и хордой следует, что

∠A₀C₀B = ∠A₀A₁B = ∠CA₁B₁ = ∠CB₁A₁ = ∠B₁C₁A₁ = ∠C₀A₀A₁,  откуда следует параллельность  BC₀ || B₁A₀.  Аналогично  BA₀ || B₁C₀.  Таким образом, BA₀B₁C₀ – параллелограмм, а значит, середина его диагонали совпадает с точкой K.

  Для других случаев расположения точек A₀ и C₀ доказательство аналогично.

  Второй способ. Поскольку  ∠BA₀I = 90°,  то согласно задаче 215617 точка A₀ лежит на биссектрисе угла A. Аналогично C₀ лежит на биссектрисе угла C (рис. справа). Медиана прямоугольного треугольника BC₀C, проведённая к гипотенузе, очевидно, параллельна AC, то есть C₀ (и аналогично A₀) лежит на средней линии треугольника ABC. Значит, AC₀A₀C – трапеция. Осталось воспользоваться замечательным свойством трапеции.

Ответ задачи отсутствует