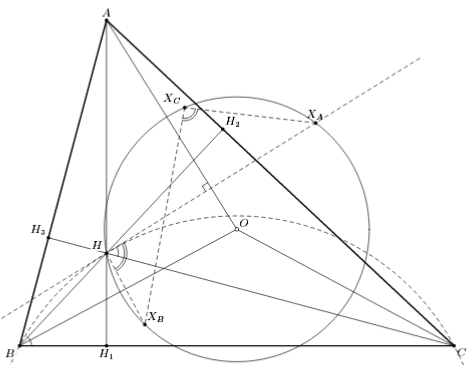
Пусть O – центр описанной окружности Ω треугольника ABC, AH₁, BH₂, AH₁, CH₃, – высоты (см. рис.). Окружность Ω_A получается из Ω параллельным переносом на вектор AH (см. решение задачи 155597). Поэтому касательная HX_A к Ω_A в точке H параллельна касательной к Ω в точке A и следовательно, перпендикулярна радиусу OA.

  Треугольник HAX_A равнобедренный, поэтому его высота совпадает с его медианой. Значит, AO – серединный перпендикуляр к отрезку HX_A. Аналогично BO, CO – серединные перпендикуляры к отрезкам HX_B, HX_C соответственно. Поэтому точки H, X_A, X_B, X_C лежат на одной окружности с центром O. Следовательно,  ∠X_AX_CX_B = ∠X_AHX_B = 180° – ∠AOB = 180° – 2∠C = ∠H₁H₃H₂.  Аналогично  ∠X_AX_BX_C = ∠H₁H₂H₃  и

∠X_BX_AX_C = ∠H₂H₁H₃.  Итак, у треугольников X_AX_BX_C и H₁H₂H₃ соответствующие углы равны, то есть они подобны.

Ответ задачи отсутствует