Назад
Задача 166355 • Сложность: 3 • 9-11 класс
Задача

Пусть R1, R2 и R3 – радиусы трёх окружностей, каждая из которых проходит через вершину треугольника и касается противолежащей стороны.

Докажите, что  1/R1 + 1/R2 + 1/R3 ≤ 1/r,  где r – радиус вписанной окружности этого треугольника.

Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2017/2018
Количество версий:
4
Решение

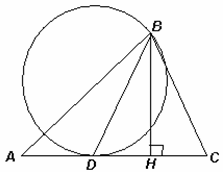
  Рассмотрим треугольник АВС и одну из указанных окружностей, которая проходит через вершину В и касается стороны АС в точке D (см. рис.). Её диаметр не меньше, чем хорда BD, которая, в свою очередь, не меньше высоты ВН треугольника.

  Таким образом,  1/2R1+1/2R2+1/2R3≤1/h1+1/h2+1/h3,  гдеhi– высоты треугольника. Осталось воспользоваться равенством  1/h1+1/h2+1/h3=1/r,  в справедливости которого легко убедиться, умножив обе части этого равенства на 2SABC.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет