Задача
Докажите, что среднее арифметическое всех делителей натурального числа n лежит на отрезке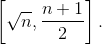 
Решение
Для n = 1 отрезок вырождается в точку, а утверждение, очевидно, верно. Далее считаем, что n > 1.
Пусть k – количество делителей числа n = a².
Оценка сверху. Количество собственных делителей равно k – 2 и каждый из них не превосходит n/2. Значит, сумма всех делителей не больше чем
n/2 (k – 2) + n + 1 = nk/2 + 1. Следовательно, их среднее арифметическое не превосходит n/2 + 1/k ≤ n/2 + ½ = n+1/2.
Оценка снизу. Пусть d1d2 = n и d1 ≠ d2, тогда, как известно,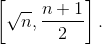 
Все делители n (кроме a, если число a – целое) разбиваются на такие пары. В любом случае d1 + d2 + ... + dk > ka. Значит, 1/k (d1 + d2 + ... + dk) > a.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь