Задача
В выпуклом четырёхугольнике АВСD точка K – середина стороны ВС, а SАВСD = 2SАKD.
Найдите длину медианы КЕ треугольника AKD, если AB = a, CD = b.
Решение
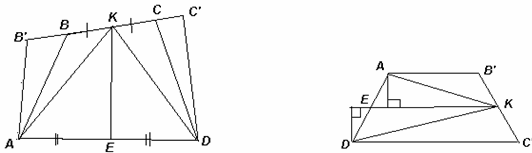
Через точки A и D проведём прямые, параллельные КЕ, до их пересечения с прямой ВС в точках B' и C' соответственно (рис. слева). Тогда AB'C'D – трапеция, а КЕ – её средняя линия.
Ответ
a+b/2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет