Олимпиадная задача: Перпендикулярные отрезки в квадрате
Задача
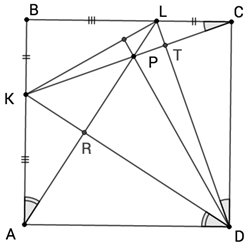
На стороне AB квадрата ABCD отмечена точка K, а на стороне BC – точка L так, что KB = LC. Отрезки AL и CK пересекаются в точке P. Докажите, что отрезки DP и KL перпендикулярны.
Решение
Пусть AL и DK пересекаются в точке R, а CK и DL – в точке T (см. рисунок). Из условия задачи следует, что ΔCBK = ΔCL (по двум катетам), значит, ∠BCK = ∠CDL. Тогда CT – высота прямоугольного треугольника DCL, поэтому KT – высота треугольника DKL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет