Назад
Задача 166372 • Сложность: 3 • 8-9 класс
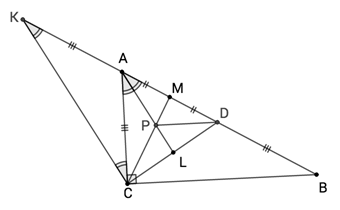
Задача

На гипотенузе AВ прямоугольного треугольника ABC отметили точку D так, что ВD = AС. Докажите, что в треугольнике AСD биссектриса AL, медиана СM и высота DH пересекаются в одной точке.

Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2017/2018
Количество версий:
4
Решение

Пусть AL и CM пересекаются в точке P (см. рисунок). Тогда утверждение задачи сводится к доказательству того, что DH проходит через точку Р.

На продолжении гипотенузы АВ отметим точку K так, чтобы AK = ВD = AС. Тогда AР – биссектриса внешнего угла при вершине равнобедренного треугольника САK, следовательно, AР || KC. Тогда по теореме Фалеса: MP:PC = MA:AK. Учитывая, что МА = MD и AK = ВD, получим: MP:PC = MD:DBDP || BC. Так как ВСAC, то DPAC, то есть DH проходит через точку P, что и требовалось.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет