Докажите, что треугольник BOC равнобедренный в трапеции ABCD
Задача
Про трапецию ABCD с основаниями AD и BC известно, что AB = BD. Пусть точка M – середина боковой стороны CD, а O – точка пересечения отрезков AC и BM. Докажите, что треугольник BOC – равнобедренный.
Решение
На луче BM за точку M отметим точку E так, что ME = MB (см. рис.). Заметим, что BCED – параллелограмм, так как его диагонали в точке пересечения делятся пополам. Тогда DE∥ BC, откуда следует, что точка E лежит на прямой AD.
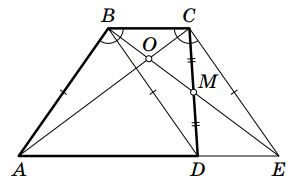
Имеем AB = BD = CE, т. е. ABCE – равнобедренная трапеция. Так как ее углы ABC и BCE равны, то треугольники ABC и ECB равны по двум сторонам (AB = EC, BC = CB) и углу между ними. Тогда равны и их соответственные углы BCA и CBE, откуда следует требуемое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь