Задача
В белом клетчатом квадрате 100×100 закрашено чёрным несколько клеток (не обязательно соседних). В каждой горизонтали или вертикали, где есть чёрные клетки, их количество нечётно, так что одна из клеток – средняя по счёту. Все чёрные клетки, средние по горизонтали, стоят в разных вертикалях. Все чёрные клетки, средние по вертикали, стоят в разных горизонталях.
а) Докажите, что найдётся клетка, средняя и по горизонтали, и по вертикали.
б) Обязательно ли каждая клетка, средняя по горизонтали – средняя и по вертикали?
Решение
а) См. задачу 167021. б) Не обязательно. На рисунке приведены примеры для квадратов 6×6 и 7×7 (В – клетка, средняя по вертикали, Г – по горизонтали, О – и по вертикали, и по горизонтали). Добавив нужное количество белых горизонталей и вертикалей, получим квадрат 100×100.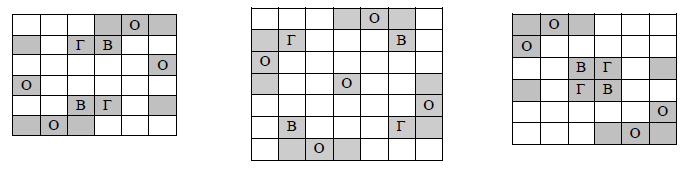 
Ответ
б) Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь