Задача
В остроугольном треугольнике $ABC$ медиана $CM$ и высота $AH$ пересекаются в точке $O$. Вне треугольника отмечена точка $D$ так, что $AOCD$ – параллелограмм. Чему равно $BD$, если известно, что $MO=a$, $OC=b$?
Решение
Возьмем на луче $CM$ такую точку $K$, что $CM=MK$. Тогда $CAKB$ – параллелограмм, т.е. $AK=BC$ и $AK\parallel BC$. Кроме того, $AO=CD$ и $\angle BCD=\angle OAK=90^{\circ}$, потому что $AH$ – высота. Следовательно, треугольники $BCD$ и $KAO$ равны, т.е. $BD=OK=2CM-CO=2a+b$.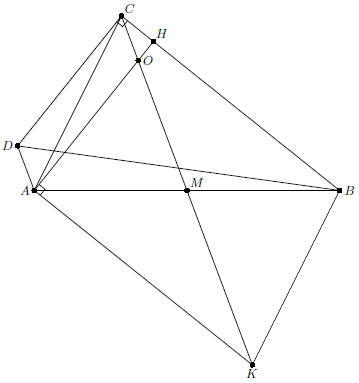
Ответ
$2a+b$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет