Задача
Крестьянин, подойдя к развилке двух дорог, расходящихся под углом 60°, спросил: "Как пройти в село NN?" Ему ответили: "Иди по левой дороге до деревни N – это в 8 верстах отсюда, – там увидишь, что направо под прямым углом отходит большая ровная дорога – это как раз дорога в NN. А можешь идти другим путём: сейчас по правой дороге; как выйдешь к железной дороге, – значит, половину пути прошёл; тут поверни налево и иди прямо по шпалам до самого NN". – "Ну, а какой путь короче-то будет?" – "Да всё равно, что так, что этак, никакой разницы". И пошёл крестьянин по правой дороге.
Сколько вёрст ему придётся идти до NN? Больше десяти или меньше? А если идти от развилки до NN напрямик? (Все дороги прямые.)
Решение
Пусть A – развилка дорог, B – деревня N, C – село NN, D – точка, где правая дорога выходит на железнодорожное полотно.
Пусть прямая BC пересекает AD в точке E, тогда ∠CED = 30°. AD = DC, поэтому ∠CDE = 2 ∠CAD < 2 ∠BAD = 120°,
∠DCE = 180° – ∠CDE – ∠CED > 30° = ∠CED. Следовательно, DC < DE, и 2AD = AD + DC < AD + DE = AE = 2AB.
Так как AB + BC = AD + DC, то согласно задаче 132883 SABC < SADC. Как показано выше, AD < AB, значит, ∠BAC < ∠DAC, то есть
∠BAC < 30°. Следовательно,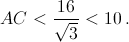 
Докажем, что длина всего пути больше 10. Для этого достаточно проверить, что AD > 5. Первый способ. Пусть ∠BAC = α, ∠CAD = β. Тогда cos α cos β = ½ (cos (α – β) + cos 60°) ≥ ¾. Из треугольника ADC получаем: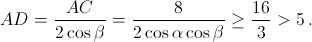 
Второй способ. Пусть AD = x, тогда BC = 2x – 8. По теореме косинусов (из треугольника ABD) BD² = x² + 64 – 8x. С другой стороны, неравенство треугольника дает BD < BC + CD = 3x – 8, откуда x² + 64 – 8x < (3x – 8)², 8x² > 40x, то есть x > 5.
Ответ
По дорогам – больше 10 вёрст, напрямик – меньше.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь