Задача
Все коэффициенты многочлена равны 1, 0 или –1. Докажите, что все его действительные корни (если они существуют) заключены в отрезке [–2, 2].
Решение
Заметим, что если q > 2, то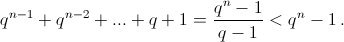 
Пусть наш многочлен P(x) имеет степень n: P(x) = xn + ... . Тогда при
|x| > 2 |P(x)| ≥ |xn| – |P(x) – xn| ≥ |xn| – (|xn–1| + |xn–2| + ... + |x| + 1) > 1 > 0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет