Пусть t_n — наименьшее число пересаживаний. Докажем, что 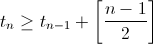    при  n ≥ 4.     (1)   Представим, что участники чаепития сидят в вершинах правильногоn-угольника. Тогда их итоговое расположение получается из исходного симметрией относительно некоторой оси. ПустьA– один из участников, наиболее удалённых от оси,B– симметричный ему. Кратчайший путь отAкBпо границе многоугольника содержит  k≥ [^n–1/₂]  сторон, поэтомуAдолжен пройти по пути кBне менееkсторон, то есть сделать не менееkпересаживаний. Но при этих пересаживаниях порядок взаимного расположения остальных  n– 1  участников не меняется и им нужно сделать ещё по меньшей мереt_n–1пересаживаний между собой, чтобы разместиться в противоположном порядке, откуда и следует (1). 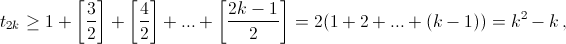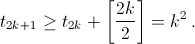Поскольку  t₃= 1,  из оценки (1) получаем, что          (2)           (3)

  Покажем, что знак неравенства в (2) и (3) можно заменить на знак равенства. Занумеруем участников чаепития по порядку от 1 до n и разобьём их на две группы – от 1-го до k-го и от (k+1)-го до n-го. Чтобы поменять порядок в первой группе, пересадим последовательно 1-го участника со 2-м, 3-м, ..., k-м, затем 2-го – с 3-м, 4-м, ..., k-м и т. д. На это уйдёт  (k – 1) + (k – 2) + ... + 1 = ½ (k² – k)  пересаживаний. Аналогично за  ½ (n – k) (n – k – 1)  пересаживаний мы получим обратный порядок во второй группе. Всего нужно  k² – k  пересаживаний при  n = 2k  и k² пересаживаний при  n = 2k + 1.

¼ (n² – 2n)  при чётном n;  ¼ (n – 1)²  при нечётном n. .