Количество делителей числа  n = 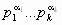  равно  (α₁ + 1)...(α_k + 1)  (см. задачу 160537 а). n делится на  30 = 2·3·5,  поэтому  k ≥ 3.  Но

(α₁ + 1)...(α_k + 1) = 30,  а 30 нельзя разложить больше, чем на три множителя, отличных от 1 (а на 3 множителя можно разложить единственным способом). Следовательно,  k = 3,  {α₁, α₂, α₃) = {1, 2, 4}.  Итак,  n = pq²r⁴,  где  (p, q, r)  – перестановка чисел  (2, 3, 5).

720, 1200, 1620, 4050, 7500, 11250.