Решение 1:   а) Возьмём  a = 2 + .  Поскольку  (2 + )(2 – ) = 1,  {a} + {¹/_a} = ( – 1) + (2 – ) = 1.   б) Допустим, что число a рационально, и представим его в виде несократимой дроби:  a = ^m/_n.  Если  {a} + {¹/_a} = 1,  то, очевидно,  a + ¹/_a  – целое число; обозначим его через k. Итак,  ^m/_n + ⁿ/_m = k,  то есть  m² + n² = kmn.  Отсюда следует, что m² делится на n, а n² – на m, а поскольку m и n взаимно просты, это возможно лишь при  |m| = |n| = 1,  то есть при  a = ±1.  Но в этом случае  {a} + {¹/_a} = 0.  Противоречие.

Решение 2:   Из условия следует, что  a + ¹/_a  – целое число, однако для несократимой дроби  a = ^p/_q  это невозможно: дробь 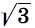    также несократима.

 Таким образом, равенство выполняется тогда и только тогда, когда  a + ¹/_a  равно целому числу n, причём a не целое. Поскольку уравнение

a² – na + 1 = 0  при  n > 2  не может иметь рациональных корней (см. задачу 161013), ответ в пункте б отрицательный.

  В качестве примера (пункт а) требуется только решить это уравнение, например, при  n = 3.

а) Например,  a = 2 + .   б) Не может.