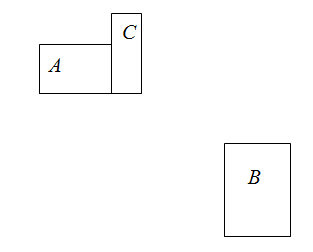
а) Будем считать, что одна из сторон квадрата вертикальна. Назовём прямоугольники связанными, если они пересекаются одной вертикальной или горизонтальной прямой. (В частности, прямоугольники, имеющие общую вершину, связаны.) Связанные прямоугольники входят в цепочку, "нанизанную" на эту прямую.

  Пусть прямоугольники A и B не связаны. Тогда (с точностью до поворота квадрата) один из них находится левее и выше другого (см. рис.).

  Рассмотрим ближайшую кBвершину прямоугольникаA. К ней примыкает (справа или снизу; далее считаем, что справа) прямоугольникС, который имеет сАобщую вершину и часть стороны. Заметим, что достаточно соединить цепочкойBиC. Действительно, если эта цепочка горизонтальна, удалим из неё все прямоугольники, лежащие левееС, заменив их наАи прямоугольники, лежащие левееАвдоль некоторой горизонтальной прямой, – получится цепочка, соединяющаяВиА. Если же эта цепочка вертикальна, то удалим из неёСи все прямоугольники, лежащие вышеС, включимАи аналогично продолжим вверх.   Для построения цепочки, соединяющейBиCрассуждение можно повторить. На каждом шаге, прямоугольники, которые нужно соединить, сближаются, так что в конце концов они станут связанными.   б) Рассуждения аналогичны. Объясним более подробно переход от параллелепипеда А к параллелепипеду C. Окрестность вершины параллелепипеда А, ближайшей в B, разбивается на восемь октантов. Один из них "занят" параллелепипедом А, а остальные распределяются по соседним параллелепипедам. При этом соседний параллелепипед может "занимать" один, два или четыре октанта. Ввиду нечётности числа 7 найдётся параллелепипед, занимающий ровно один октант (он может иметь с А только общую вершину или общие вершину и часть грани). В любом случае, соединив его цепочкой с B, мы сможем "переделать" эту цепочку, в цепочку, соединяющую А и B.

Ответ задачи отсутствует