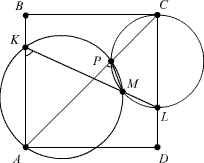
Пусть точка M лежит внутри треугольника ACD. Обозначим через P вторую точку пересечения диагонали AC с описанной окружностью треугольника AKM. Тогда точки K и P лежат по одну сторону от прямой AM, значит,  ∠AKM = ∠APM  (как вписанные, опирающиеся на одну дугу). Точки P и L лежат по разные стороны от прямой CM, и  ∠MPC + ∠MLC = (180° – ∠APM) + ∠AKM = 180°.  Следовательно, четырёхугольник CLMP вписанный, то есть точка P лежит и на описанной окружности треугольника MLC.

  Случай, когда точкаMлежит внутри треугольникаABC, разбирается с точностью до "наоборот".   Если же точкаMлежит наAC, то указанные описанные окружности касаются в точкеM(то есть вторая точка пересечения отсутствует).   Действительно, в этом случае гомотетия с центромM(и коэффициентом   –^MC/_MA) переводит треугольникAKMв треугольникCLM. Поэтому та же гомотетия переводит центр первой описанной окружности в центр второй. Следовательно, общая точка этих окружностей лежит на линии центров и, значит, являет точкой касания.

Ответ задачи отсутствует