Олимпиадная задача: пары (a, b) с делимостью в теории чисел для 8-9 класса

Олимпиадная задача по теории чисел: делимость и конструкции для 8-9 класса

Задача

Доказать, что существует бесконечно много таких пар (a, b) натуральных чисел, что a² + 1 делится на b, а b² + 1 делится на a.

Решение

Решение 1:Заметим, что если a < b, a² + 1 = cb, b² + 1 = da, (a, b) = 1, то 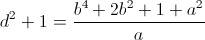кратно b. Значит, из "хорошей" пары (a, b) можно получить новую хорошую пару (b, d), причём b < d, (b, d) = 1. В качестве первой пары можно взять (1, 2).

Решение 2:Для знатоков. Используем известное свойство чисел Фибоначчи: 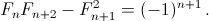Подставляя F_n+1 = F_n+2 – F_n, получим 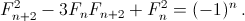Отсюда видно, что при нечётном n пара (F_n, F_n+2) удовлетворяет условию.