Олимпиадная задача по комбинаторной геометрии для 7–9 классов: перекрашивание треугольников
Задача
Правильный треугольник разбит прямыми, параллельными его сторонам, на равные между собой правильные треугольники. Один из маленьких треугольников чёрный, остальные – белые. Разрешается перекрашивать одновременно все треугольники, пересекаемые прямой, параллельной любой стороне исходного треугольника. Всегда ли можно с помощью нескольких таких перекрашиваний добиться того, чтобы все маленькие треугольники стали белыми?
Решение
Нетрудно проверить, что если исходный треугольник разрезан на четыре треугольничка, то сделать все треугольнички белыми можно.
Докажем, что при большем числе частей этого сделать нельзя. Рассмотрим четыре треугольничка с общей вершиной, составляющих два ромбика (см. рис.).
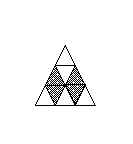
Ответ
Не всегда.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь