Олимпиадная задача по алгебраическим неравенствам: таблица и сумма зачеркнутых чисел
Задача
Дана таблица n×n, заполненная числами по следующему правилу: в клетке, стоящей в i-й строке и j-м столбце таблицы записано число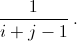 
В таблице зачеркнули n чисел таким образом, что никакие
два зачёркнутых числа не находятся в одном столбце или в одной строке.
Докажите, что сумма зачёркнутых чисел не меньше 1.
Решение
Решение 1: Сумма чисел, стоящих в левой верхней и правой нижней вершинах любого прямоугольника, больше суммы чисел, стоящих в других двух вершинах:
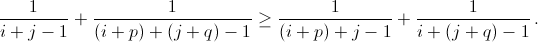Действительно, это неравенство имеет вид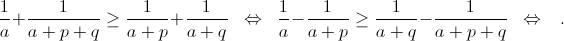 
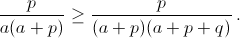
Если в левой нижней клетке таблице число не зачёркнуто, то берём зачёркнутые числа, стоящие в первом столбце и n-й строке, рассматриваем прямоугольник, диагональ которого они образуют и заменяем их на числа, стоящие в других двух вершинах прямоугольника. При этом сумма зачёркнутых чисел уменьшится, а в левой нижней клетке таблицы появится зачёркнутое число. Выкинув из таблицы первый столбец и n-ю строку, повторим процедуру с уменьшенной таблицей и т. д.
В результате получим таблицу, в которой зачёркнуты все числа по диагонали, ведущей из левого нижнего в правый верхний угол.
Сумма этих чисел равна 1.
Решение 2:
Пусть вычеркнуты клетки с номерами (1, i1), (2, i2), ..., (n, in). Положим ak = k + ik – 1 – это знаменатели вычеркнутых дробей. Заметим, чтоa1 + ... + an = (1 + i1 – 1) + (2 + i2 – 1) + ... + (n + in – 1) = (1 + ... + n) + (i1 + ... + in) – n = 2(1 + ... + n) – n = n(n + 1) – n = n².
Согласно неравенству между средним арифметическим и средним гармоническим (см. задачу 161402 в)
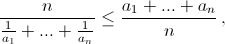то есть
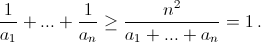
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь