Олимпиадная задача: Существует ли выпуклый пятиугольник с подобным отрезаемым пятиугольником?

Решение 1:На рис. слева изображен пятиугольник с углами 60° и 120° и сторонами 2, 4, 8, 6, 12. У отсекаемого подобного пятиугольника все размеры в два раза меньше.

           

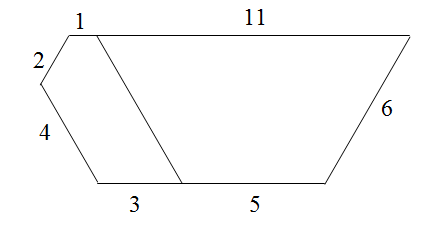
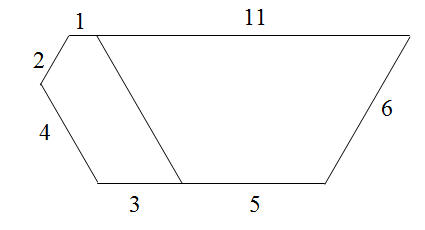
Решение 2:Будем рассматривать пятиугольники, в которых все углы равны. Нетрудно понять, что если три последовательные стороны одного такого пятиугольника пропорциональны трем сторонам другого, то эти пятиугольники подобны. Пусть ABCDE – такой пятиугольник со сторонами  AB = a,  BC = ka  и  CD = k²a,  где  ⅔ < k < 1  (рис. справа). Так как  BC > CD,  то  ∠DBC < ∠BDC.  Следовательно,  ∠ABD > ∠EDB,  то есть  ED > AB.  Поэтому на ED найдётся такая точка E₁, что  DE₁ = k³a.  Проведя через E₁ прямую, параллельную AE, до пересечения с AB в точке A₁, получим пятиугольник BCDE₁A₁, подобный ABCDE.

Существует.