Олимпиадная задача: сколько цветов нужно для раскраски клетчатого листа с условиями на расстояния и фигуры?
Задача
В какое наименьшее число цветов нужно раскрасить клетки бесконечного листа клетчатой бумаги, чтобы
а) каждые две клетки на расстоянии 6 были покрашены в разные цвета? б) каждые четыре клетки, образующие фигуру формы буквы Г, были покрашены в четыре разных цвета? (Расстояние между клетками – наименьшее число линий сетки, горизонтальных и вертикальных, которые должна пересечь ладья на пути из одной клетки в другую.)
Решение
а) См. задачу 197823. б) Пример восьмицветной раскраски показан на рис. слева.
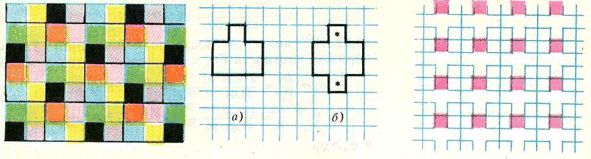
Ответ
а) В 4 цвета; б) в 8 цветов.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет