Олимпиадная задача: Ладья и шахматная доска — доказательство для 9-11 классов

Решение 1:   Предположим противное: ладье удалось обойти доску, сделав 32 горизонтальных и 32 вертикальных хода. Соединив центры полей в порядке обхода их ладьей, получим замкнутую ломаную с углами 90° между звеньями. Поскольку область D, ограниченная такой ломаной, не содержит ни одного поля целиком, на ломаной обязательно имеется двойной поворот (рис. слева; см. решение задачи 198365), причём такой, что "узел" a находится внутри D.

  Закроем среднюю часть двойного поворота доминошкой 1×2. При этом в ломаной образуется разрыв, который можно устранить, "связав" оборванные звенья (рис. в центре). При этом длина ломаной уменьшится на 2, причем если на доске появиласьвертикальнаядоминошка (как на рисунке), то стало меньше на двагоризонтальныххода и наоборот. На новой ломаной снова есть двойной поворот. Поступим с ним аналогично и т. д. Описанную процедуру можно повторять до тех пор, пока ломаная не превратится в единичный квадрат (рис. справа). Так как стало меньше на 30 вертикальных и 30 горизонтальных ходов, то на доске появилось 15 горизонтальных и 15 вертикальных доминошек. Оставшийся квадрат закроем двумя вертикальными доминошками. В результате мы получим разбиение шахматной доски на доминошки, в котором вертикальных доминошекнечётноечисло.   Нотакое разбиение невозможно– см. задачу188042.

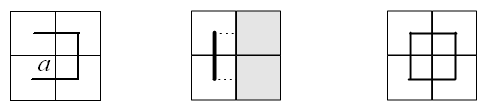
Решение 2:   Рассмотрим координатную сетку, узлы которой соответствуют центрам полей доски (теперь все вершины многоугольника D лежат в узлах). По известной формуле Пика (см. задачу 158208) площадь S области D равна  n + ^m/₂ – 1,  где n – количество узлов, находящихся внутри D, а m – количество узлов, находящихся на её границе. В нашем случае  n = 0,  m = 64,  то есть S = 31.

  Рассмотрим полосатую раскраску доски: нечётные горизонтали – чёрные, чётные – белые. Разрежем область D на прямоугольники ширины 1, проведя вертикальные прямые через центры всех полей. Каждый из них ограничен сверху и снизу горизонтальными отрезками-ходами. Площадь каждого прямоугольника – целое число, причем оно нечётно тогда и только тогда, когда ограничивающие его горизонтальные ходы находятся в горизонталях разного цвета.

  Поскольку площадь S нечётна, количество прямоугольников нечётной площади нёчетно. Значит, нечётно и количество k ходов, сделанных в чёрных горизонталях (такие ходы "входят" по одному в прямоугольники нечётной площади и по два в некоторые прямоугольники чётной площади).

  Всего из 32 чёрных полей сделано 32 хода. При этом k из них (горизонтальных) сделаны снова на чёрные поля, а  32 – k  (вертикальных) – с чёрных полей на белые. Но ладья после обхода доски вернулась на поле того же цвета, поэтому количество ходов с чёрных полей на белые равно количеству ходов с белых полей на чёрные. Таким образом количество всех вертикальных ходов равно  64 – 2k,  а количество горизонтальных ходов равно 2k и, следовательно, не может равняться 32 (ведь k нечётно).

Ответ задачи отсутствует