Олимпиадная задача по планиметрии: независимость длины AK, 8-10 класс

Задача

D– точка на сторонеBCтреугольникаABC. B треугольникиABD, ACDвписаны окружности, и к ним проведена общая внешняя касательная (отличная отBC), пересекающаяADв точкеK. Докажите, что длина отрезкаAKне зависит от положения точкиDнаBC.

Решение

Обозначим точки касания, как показано на рисунке.

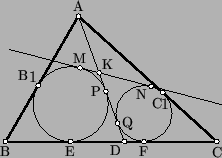
Заметим, что AB₁ = AP, AC₁ = AQ, KM = KP, KN = KQ. Кроме того, MN = EF – отрезки общих касательных к окружностям. Поэтому

2AK = (AP – KP) + (AQ – KQ) = AP + AQ – MN = AB₁ + AC₁ – EF = AB – BB₁ + AC – CC₁ – (BC – BE – CF) = AB + AC – BC.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: докажите независимость длины AK в треугольнике ABC

Задача

Решение

Ответ

Подтверждение удаления