Олимпиадная задача по планиметрии: площадь вписанного четырёхугольника (8-9 класс)
Задача
Во вписанном четырёхугольнике ABCD длины сторон BC и CD равны. Докажите, что площадь этого четырёхугольника равна ½ AC² sin∠A.
Решение
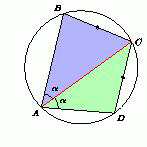 Рассмотрим треугольник AEC, равный треугольнику CDA (точки B и E находятся по разные стороны прямой AC). Поскольку ∠ACE = ∠CAD = ∠BAC, то
Рассмотрим треугольник AEC, равный треугольнику CDA (точки B и E находятся по разные стороны прямой AC). Поскольку ∠ACE = ∠CAD = ∠BAC, то
AB || CE. Кроме того, AE = CD = BC, то есть ABCE – равнобедренная трапеция. Угол между её диагоналями равен 2∠BAC = ∠A, и согласно задаче 154962 SABCD = SABCE = ½ AC² sin∠A.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет