Олимпиадная задача по планиметрии для 8–9 классов от Назарова Ф.

  а) По условию  AC < BC,  следовательно,  AB < AC + ВC < 2ВС.   б) Из двух точек A и D выберем ту, которая расположена ближе к прямой BC (если расстояния одинаковы, то выберем любую из них). Пусть это будет точка A (см. рис.). 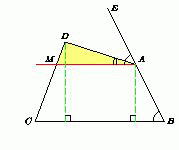  На продолжении отрезкаABза точкуAвозьмём точкуE. Через точкуAпроведём прямую, параллельнуюBC. ПустьM– точка пересечения этой прямой с прямойDC. ЧетырёхугольникABCM– трапеция, причём  ∠B+ ∠C< 180°  (так как  ∠A+ ∠B+ ∠C+ ∠D= 360°  и  ∠A+ ∠D> ∠C+ ∠B).  Отсюда следует, что  AM < BC.  ЛучADпроходит между сторонами углаEAMили совпадает с лучомAM(в силу выбора точкиA). Поэтому   ∠DAM< ∠EAM= ∠ABC< ∠D.   Применяя к треугольникуDAMутверждение пункта а), получим, что  AM> ½AD,  а так как  AM < BC,  то  BC> ½AD.

Ответ задачи отсутствует