Олимпиадная задача по планиметрии: точка пересечения медиан в треугольнике, 8-9 класс
Задача
Пусть M – точка пересечения медиан треугольника ABC .
На перпендикулярах, опущенных из M на стороны BC , AC и AB , взяты точки A1, B1и C1соответственно,
причём A1B1 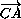 MC и A1C1
MC и A1C1 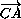 MB .
Докажите, что точка M является точкой пересечения медиан и
в треугольнике A1B1C1.
MB .
Докажите, что точка M является точкой пересечения медиан и
в треугольнике A1B1C1.
Решение
Обозначим
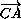 =
= ,
,
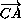 =
=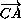 ,
,
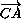 =
=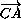 ,
,
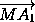 =
=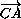 ,
,
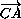 =
= ,
,
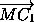 =
=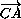 .
.
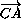 =
= 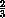
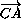 =
=
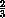 ·
· 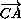 (
(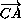 +
+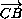 )=
)=
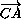 (
(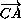 -
- ),
),
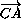 =
= 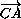 -
- ,
,
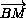 =
= 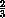
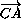 =
=
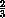 ·
· 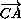 (
(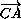 +
+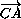 )=
)=
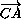 (
( -
-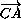 ),
),
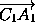 =
= 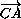 -
-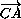 .
.
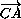 ·
· 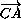 =
=
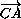 ·
·  =
=
 ·
· 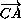 = 0,
= 0,
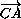 -
- )·
(
)·
(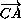 -
- ) =
) =
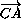 · 3
· 3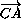 =
3
=
3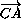 ·
· 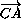 =0,
=0,
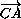 -
-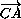 )·
(
)·
( -
-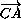 ) =
) =
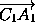 · 3
· 3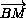 =
3
=
3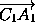 ·
· 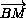 = 0
= 0 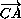
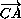
 ·
·  +
+ 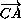 ·
· 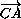 =
=
 ·
· 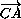 +
+ 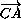 ·
· 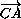 =0.
=0.
 =-
=-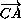 -
-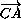 и
и 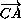 =-
=-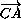 -
- , то
, то
 ·
·  +
+ 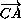 ·
· 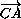 =
(-
=
(-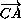 -
-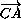 )·
)·  +
(-
+
(- -
-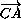 )·
)· 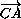 =
-
=
-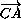 ·
·  -
- 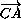 ·
· 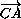 .
.
 ·
· 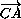 +
+ 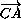 ·
· 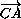 =
(-
=
(-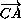 -
-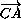 )·
)· 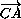 +
(-
+
(- -
-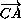 )·
)· 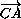 =
-
=
-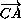 ·
· 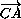 -
- 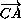 ·
· 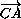 .
.
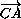 +
+ +
+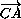 =
=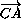 (отсюда будет следовать, что M – точка пересечения медиан треугольника A1B1C1).
(отсюда будет следовать, что M – точка пересечения медиан треугольника A1B1C1).
Действительно,
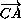 · (
· (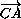 +
+ +
+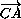 ) =
) =
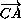 ·
· 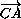 +
+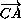 ·
· 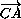 =0,
=0,
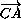 · (
· (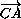 +
+ +
+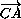 ) =
) =
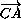 ·
· 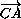 +
+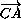 ·
·  =0,
=0,
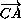 и
и 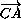 неколлинеарны, то
неколлинеарны, то 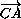 +
+ +
+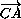 =0
=0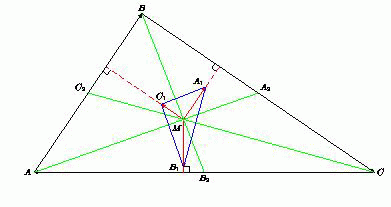
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет